Researchers find overlooked weakness in powerful machine learning tool

In nonlinear dynamic systems, a change in one place can trigger an outsized change elsewhere. The climate, the workings of the human brain, and the behavior of the electric grid are all examples—and all change dramatically over time. Because of their inherent unpredictability, dynamic systems like these are notoriously difficult to model.

In the last two decades, however, researchers have reported success modeling high-dimensional chaotic behaviors with a simple but powerful machine-learning approach called reservoir computing.

“Machine learning is increasingly being used to learn some complex dynamic systems that we don’t have a good mathematical description for from data,” says Yuanzhao Zhang, an SFI Complexity Postdoctoral Fellow.

Recent papers, he says, have reported that reservoir computing is effective in predicting the trajectory of chaotic systems after seeing very little training data, and can even determine where the system would end up just from its initial conditions. Zhang was excited, but also skeptical.

“And those reports made me wonder, can this be true?” Asks Zhang.

The answer he found is—sort of. In a new paper in Physical Review Research, Zhang and his collaborator, physicist Sean Cornelius at Toronto Metropolitan University, identify limitations to reservoir computing that, Zhang says, have been overlooked by the research community so far—and suggest a kind of Catch-22 that can prove hard to circumvent, especially for complicated dynamic systems.

“It’s one of those limitations that I think hasn’t been very well appreciated by the community,” says Zhang.

First proposed by computer scientists more than 20 years ago, reservoir computing (RC) is a nimble predictive model, built with neural networks, that is both simple and cheaper to train than other neural net frameworks.

In 2021, researchers introduced next-generation reservoir computing, or NGRC, that confers several advantages over conventional RC, including requiring less data to train. Recent studies exploring its use in machine learning applications suggest that RC and NGRC models can be powerful in modeling dynamic systems using little data.

Zhang and Cornelius examined both standard RC and NGRC, and found them wanting in certain common situations. “They both have a Catch-22 problem, but they’re different problems.”

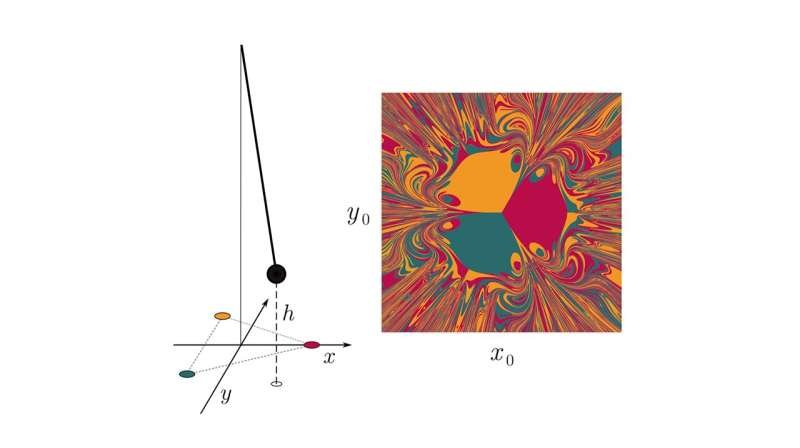
For the NGRC, the duo looked at a simple dynamic chaotic system—a pendulum with a magnet attached at the end, swinging among three magnets fixed in a triangle on a flat surface. They found that if they gave the system information about the type of nonlinearity needed to describe the system, then it performed well.

“In a sense, you have this kind of information sneaked in before the training begins,” he says. And if they perturbed the model? “Generally, it performed really poorly,” Zhang says. That suggests that the model cannot make accurate predictions unless key information about the system being predicted was already built in. For RC, the duo observed that in order to correctly predict the system, the model requires a lengthy “warm-up” time that’s almost as time-consuming as the dynamic movements of the magnet itself.

Addressing these limitations in both RC and NGRC, he says, could help researchers better use this emerging computing framework.